Контурные графики

В этом разделе рассматриваются контурные графики функций двух перемен­ных, для построения которых применяется функция contour. Контурные гра­фики, широко применяющиеся в контексте оптимизации функций, позволяют отобразить рельеф функции двух переменных так, что местонахождение опти­мума становится очевидным.

Допустим, определена функция f от n переменных f (x) = f (x₁,... ,x_n) и x∈  ℝⁿ, Для заданного а ∈  ℝⁿ уравнение

f (x) = а                               (2)

определяет поверхность в (n + 1)-мерном пространстве ℝ^п+1,

При n = 2 точки z = f (x₁,x₂) представляют поверхность в трехмерном про­странстве (x₁,x₂, z) ∈  ℝ³, что позволяет отобразить контурный график целевой функции. При n > 3 столь удобного решения не существует - в этом случае мож­но выбрать две наиболее значимые переменные и построить график, варьируя только их.

Функция contour, позволяющая построить контурный график, использует следующий синтаксис:

contour(  х,  у,   z,  nz )

где

• х и у - векторы-строки значений x и у, с числом элементов nl и п2 соот­ветственно;
• z вещественнозначная матрица размером (n1,n2), содержащая значения рассматриваемой функции, либо функции Scilab, определяющая поверхность z=f(x,y).
• nz – значения уровней или количество уровней.

В следующем фрагменте мы используем простую форму функции contour, которой в качестве параметра передается функция myquadratic. Функция myquadrat принимает два аргумента xl и х2 и возвращает значение f(х₁,х₂) =x21+x22  - Функция linspace используется для генерации значений переменных, так что функция анализируется в двухмерном  интервале [—1,1]².

function  f  = myquadratic2arg (xl , x2)

f  = xl**2 + x2**2;

endfunction

xdata = linspace (-1,1, 100 ) ;

ydata = linspace (-1,1, 100 ) ;

contour   (  xdata,   ydata,   myquadratic2arg , 10)

Полученный в результате график представлен на рис. 11.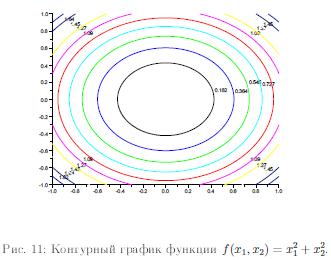

На практике функция, график которой необходимо отобразить, часто при­нимает единственный аргумент х, представляющий собой вектор-строку, в то время как функция contour требует наличия двух аргументов. Можно предло­жить следующие варианты решения данной проблемы:

• определить новую функцию, которая будет вызывать исходную,
• передать функции contour массив данных вместо объекта-функции.

Оба этих подхода рассмотрены в текущем разделе, так что читатель может выбирать наиболее подходящий вариант.

Ниже рассматривается пример построения графика квадратичной функции myquadraticlarg, принимающей вектор из двух элементов в качестве своего единственного аргумента. Для вычисления матрицы zdata, содержащей зна­чения функции, выполняются два вложенных цикла. Для каждой комбинации (х(i),у(j)) ∈  ℝ²при i = 1, 2,...,n_x и j = 1,2,...,n_y, где n_x и n_y - это ко­личество точек по осям х и y соответственно, в матрицу zdata заносится со­ответствующее значение. Наконец, для построения графика, мы обратимся к функции contour,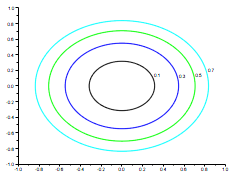

Рис. 12: Контурный график f(х₁, х₂) =x21+x22 , с явным указанием уровней.

передав ей список уровней (а не их число, как в предыду­щем фрагменте). Это позволяет явно задать требуемые уровни вместо того, чтобы предоставлять Scilab их автоматическое вычисление.

function  f  = myquadraticlarg(х)

f  = х(1)**2 + х(2)** 2; endfunction

xdata = linspace (-1,1, 100 ) ;

ydata =  linspace   (-1,1,100  ) ;

// Внимание ! Применения двух вложенных циклов следует избегать for  i =  1:length(xdata)

for  j   =  1:length(ydata)

x =   [xdata(i)   ydata(j)].';

zdata ( i,  j )  = myquadraticlarg (x);

end

end

contour   (  xdata,   ydata,   zdata,   [0.1   0.3  0.5 0.7])

Полученный график показан на рис. 12.

Рассмотренный фрагмент выполняет поставленную задачу, однако работа­ет неэффективно из-за использования циклов. Для повышения скорости вы­полнения использованию циклов следует предпочесть применение встроенных функций и векторизованных операций, рассмотренных ранее.

В следующем примере мы воспользуемся инструкцией feval, которая вы­числяет значения функции на сетке, образованной декартовым произведени­ем двух интервалов, так что полученная сетка содержит все комбинации зна­чений (х(i),у(j)) ∈  ℝ². В данном случае предположим, что модифицировать функцию myquadraticlarg невозможно, поэтому определим промежуточную функцию myquadratic3, принимающую два входных аргумента и вызавающую myquadraticlarg. Теперь, используя встроенную функцию feval, можем получить матрицу значения значений функции zdata.

function  f  = myquadraticlarg( x )

f  = x(l)**  2 + x(2)** 2; endfunction

function  f  = myquadratic3 (xl, x2)

f  = myquadraticlarg( [xl  x2] ) endfunction

xdata =  linspace   (-1,1,100  ) ;

ydata =  linspace   (-1,1,100  ) ;

zdata =  feval   ( xdata,   ydata,   myquadratic3 );

contour   (  xdata,   ydata,   zdata,   [0.1   0.3  0.5 0.7])

В результате получим тот же контурный график, что и ранее (рис. 12).

Наконец, построить график функции myquadratic3 также можно, непосред­ственно передав эту функции в качестве аргумента contour:

function  f  = myquadraticlarg (  x )

f  = x(l)**  2 + x(2)** 2; endfunction

function  f  = myquadratic3 (xl, x2)

f  = myquadraticlarg ( [xl  x2] ) endfunction

xdata = linspace (-1,1, 100 ) ;

ydata = linspace (-1,1, 100  ) ;

contour   (  xdata,   ydata,  myquadratic3,   [0.1  0.3  0.5 0.7])

В результате получим тот же контурный график, что и ранее (рис. 12). Пре­имуществом этого способа является экономия памяти, так как нам в данном случае не приходится хранить матрицу значений функции zdata.

Мы рассмотрели вкратце построение простых двухмерных графиков. В сле­дующем разделе мы обратимся к возможностям настройки таких элементов графика, как заголовок, названия осей и легенда.